by Allyson Lewis p.21, Bob Teagarden notes...
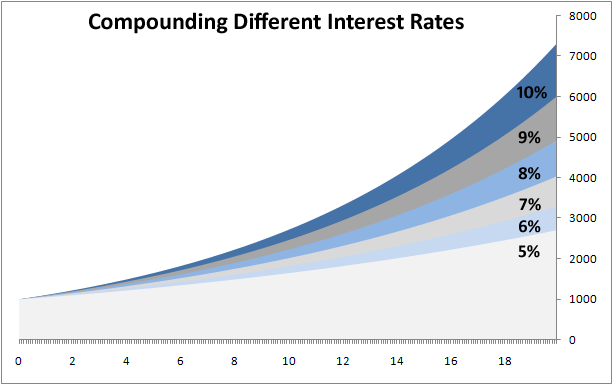
The quote itself can be found today in various collocations and variations and some even go as far as to dispute if the words were even said, but considering the Einstein is also attributed as being the man who discovered the Rule of 72, we would like to give history the benefit of the doubt. Compound interest can in fact be calculated rather simply.
The Rule of 72 is a useful calculation for working out how long it will take for an investment to double. The calculation very simply allows you to calculate compound-interest given the variable of % rate of return (ROR) or tenor (length of investment), if you need to calculate the necessary return to double your money in a given time-frame or want to know how long it will take given a specified rate of return.

For example: if you were to invest 100 Yen with a compounding interest rate of 9% per annum, the rule of 72 gives 72/9= 9 years required for the investment to be worth 200 Yen.
To determine the necessary rate of return to double a sum within a given time-frame we simply work from the other end..
For example: if you wish for your 100 Yen to be 200 Yen in 12 years time the rule of 72 gives us 72/12 = 6% of necessary rate of return each year. Accordingly, the Rule of 72 can be used as a simple way to make approximate mental calculations of otherwise complex compound-interest calculations.
For example: If I need to calculate what rate of return would be necessary to turn a 1,000,000 Dollar investment into a 3,600,000 Dollar investment in 10 years I would proceed as follows:
– as a rule of thumb 7.2% @ 10 years (72/10) = 200% return
– 3,600,000 is almost x4 times larger than 1,000000
so
we could say that we require approximately twice (a little bit less in fact) the ROI required to produce 200% which would give us an ROI of 14.2% (7.2% x 2). Again, this will be an approximation so accordingly you would want to lessen this figure (we dont need a full x4 times the original) so we could feasibly guesstimate at 13%…
Calculation would illustrate that we would actually need an ROI of 13.67% to take us to our target sum.
In summary, the rule of 72 can be an extremely resourceful tool for working out the doubling time of a principal, acted upon by compound interest and can also (if you’re comfortable with guesstimating) provide you with a ballpark ROI for non-doubling mental calculations also.
Why not download our simple Excel calculator to see the effect of compounding interest on variables of your choosing.